进入高中，学习数学的第一课，就是集合。集合作为近代数学中的一个重要数学概念，它不仅与高中数学的许多内容有着紧密的联系，而且已经渗透到自然科学的众多领域，应用十分广泛。掌握好集合的知识既是数学学习本身的需要，也是全面提高数学素养的一个必不可少的内容。因此，今天我们就来讲讲集合这一块主要内容。

　　正确理解集合的概念：

　　研究一个集合，首先要看集合中的代表元素，然后再看元素的限制条件，当集合用描述法表示时，注意弄清其元素表示的意义是什么．注意区分{x|y＝f(x)}、{y|y＝f(x)}、{(x，y)|y＝f(x)}三者的不同。

　　注意空集的特殊性：

　　空集是不含任何元素的集合，空集是任何集合的子集．在解题时，若未明确说明集合非空时，要考虑到集合为空集的可能性．例如：A⊆B，则需考虑A＝∅和A≠∅两种可能的情况。

　　典型例题1：

　　元素与集合

　　1、集合中元素的三个特性：确定性、互异性、无序性．

　　2、集合中元素与集合的关系：

　　元素与集合之间的关系有属于和不属于两种，表示符号为∈和∉.

　　在进行集合的运算时要尽可能地借助Venn图和数轴使抽象问题直观化．一般地，集合元素离散时用Venn图表示；集合元素连续时用数轴表示，用数轴表示时注意端点值的取舍．

　　在解决有关A∩B＝∅，A⊆B等集合问题时，一定先考虑A或B是否为空集，以防漏解．另外要注意分类讨论和数形结合思想的应用．

　　典型例题2：

　　研究集合问题，一定要抓住元素，看元素应满足的属性，对于含有字母的集合，在求出字母的值后，要注意检验集合的元素是否满足互异性．

　　对于集合相等首先要分析已知元素与另一个集合中哪一个元素相等，分几种情况列出方程(组)进行求解，要注意检验是否满足互异性．

　　常见集合的符号表示：

　　集合间的基本关系

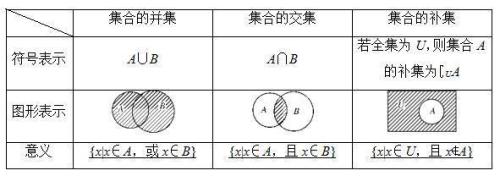
　　集合的基本运算

　　典型例题3：